What is Sampling Variation?
What is Sampling Variation?
Introduction
In this blog post, I want to pay attention to the concept of sampling variation. In my econometrics classes, I have often found that students have a hard time wrapping their heads around this concept, especially in the case of regression analysis. Some of the questions I often get range from “why is our estimate of \(\beta\) uncertain, since we have obtained it in a deterministic way from our data sample” to “where do \(t\) statistics come from?”.
In this blog post, I explain the fundamental concept responsible for why our estimate of \(\beta\) is uncertain, and how to characterize (meaning, put probabilities on it) this uncertainty: the concept of sampling variation. In this characterization, we’ll also focus on the origins of the \(t\) distribution used for hypothesis testing.
Basics of Sampling Variation
Be that as it may, the basic concept of sampling variation is very easy to grasp.
Consider a series of i.i.d. normally distributed random variables \(X_i\) (indexed by the \(i\)’th observation), distributed with mean \(\mu\) and variance \(\sigma^2\). This means that we pretend that all of our data points are generated by such a normal distribution, and each observation in our dataset is generated by that very same distribution, irrespective of preceding or subsequent data points.
As an econometrician, it’s your job to estimate the \(\mu\) and \(\sigma^2\) parameters of that normal distribution based on a finite sample of \(N\) observations. The following piece of R code illustrates that:
# Load libraries, set seed for reproducability
library(tidyverse, quietly = TRUE)
set.seed(1234)
# Set parameters for our normal distribution and sample size
mu <- 5; sigma_sq <- 1; n <- 20
# Sample from this "true" population distribution
sample <- tibble(data=rnorm(n=n, mean=mu, sd=sqrt(sigma_sq)))
head(sample, 5)
## # A tibble: 5 × 1
## data
## <dbl>
## 1 3.79
## 2 5.28
## 3 6.08
## 4 2.65
## 5 5.43
mean(sample$data)
## [1] 4.749336
As you can see, we have sampled from a normal distribution with \(\mu=5\). However, our estimated mean is only 4.7493359.
Because you have only twenty data points, the probability of you getting exactly 5 as an estimate for your \(\mu\) is very small (in fact, it’s zero). In addition, there is a certain probability of you sampling exclusively very high-valued data points and your estimated mean being way higher than five. Similarly, there is a certain probability of sampling low-valued data points, making your estimated mean way lower than five.
All of this can happen precisely due to coincidence. The process of putting certain numbers on these probabilities is the process of deriving the sampling distribution. After we have found the sampling distribution, we can use it to quantify the uncertainty that we attach to a certain estimate.
One particular parameter governing the sampling distribution is the sample size \(N\). It turns out, as we will see, that the larger the sample size, the lower the probability of sampling only extreme data points.
If you don’t understand this, consider repeated fair coin flips. The probability of receiving 3 out of 3 heads (a sample size of 3) is larger than the probability of receiving 10 out of 10 heads (a sample size of 10). Which in turn is smaller than the probability of receiving 100 out of 100 heads. Et cetera.
Similarly, if our true normal distribution has \(\mu=5\), the probability of, for example, observing only observations that are higher than, say, 6, becomes smaller and smaller as our sample size increases.
Technically, the probability of drawing an observation greater than 6 from our normal random variable \(\mathcal{N}(5, 1)\) is:
p_greater_than_6 <- 1 - pnorm(6, mean=mu, sd = sqrt(sigma_sq))
So about 15%. The probability that two observations are both greater than six is:
p_greater_than_6^2
## [1] 0.02517149
So only 2%, because our observations are independently distributed.
Because the probability of sampling only extreme observations decreases with the sample size, this means that, if your sample is very large, you’re bound the end up with an estimate of \(\mu\) that is fairly close to the real population parameter.
Deriving Sampling Variation: Example
Let us now derive more explicitly the sampling distribution of the around the parameter \(\mu\).
We know that we estimate the mean by:
$$ \bar{X} = \frac{1}{N} \sum_{i=1}^N X_i $$
We also know that each \(X_i\) has expected value equal to the population mean \(\mathbb{E}[X_i]=\mu\) and variance \(\sigma^2\).
Let us now consider the sum of independent normal variables. Let’s call that \(S\) for a second:
$$ S = \sum_{i=1}^N X_i $$
We know that the \(S\) is also normally distributed as it is a combination of i.i.d. normal distributions, and let us now derive the \(\mu\) and the \(\sigma^2\) of the \(S\), that is, of the normal distribution that arises from the sum of \(N\) i.i.d. normal random variables.
Since all of the \(N\) i.i.d. normals have the same expectation, \(\mu\), \(S\) will have the expected value \(N \mu\). Since all of them are independent, and have the same variance, the variance of the \(S\) will equal \(N \sigma^2\).
Since the sample mean \(\bar{X}\) is just the sum divided by \(\frac{1}{N}\), the sample mean \(\bar{X}\) will also follow a normal distribution. The \(\mu\) of that distribution, denoted as \(\mu_{bar{X}}\) is just:
$$ \mu_{\bar{X}} = \frac{1}{N} \mu_S $$
where \(\mu_S\) is the mean of \(S\), which we have seen to equal \(N \mu\). Hence, the expected value of the sample mean \(\bar{X}\) is \(\mu\). That is a good thing! This means that the sample mean is an unbiased estimator of the population mean.
As for the variance, remember the rule that: \(\text{Var}(aZ)= a^2 \text{Var}(Z)\) for any random variable \(Z\). In this case, the variance of \(\bar{X} = \text{Var}(\frac{1}{N} S)\).
This equals:
$$ \sigma^2_{\bar{X}} = \frac{1}{N^2} \text{Var}(S) = \frac{1}{N^2} N \sigma^2 = \frac{1}{N} \sigma^2 $$
Hence, what we have derived is that the sample mean is distributed as:
$$ \bar{X} \sim \mathcal{N}(\mu, \frac{1}{N} \sigma^2) $$
This is very nice. That means that as the sample size grows, we’re obtaining a distribution around the population mean with a smaller and smaller variance. This formally illustrates what I argued anecdotally earlier: the probability of estimating an extreme sample mean (in the sense of being far away from the population mean) decreases with \(N\).
The other parameter that governs the uncertainty of our sample mean is \(\sigma^2\). If our variables we sample have higher true population variance, the probability of achieving more extreme draws (again meaning, a sample mean far away from the population mean) is higher. Hence, this would imply more uncertainty around our estimate.
Hypothesis Testing
Using the sampling distribution, and in particular, the variance can also be useful for hypothesis testing. I’ll get back to this in the case of linear regression, but a hypothesis test is nothing else than asking:
Given a value for
\(\mu\)under the null hypothesis and the variance of the sampling distribution, what is the probability of obtaining a sample mean that I have actually obtained, or something more extreme?
This is precisely the definition of a \(p\) value.
In my simulated example above, I can test H0 of the population mean being equal to, say, four against the alternative hypothesis of it being \(\neq 4\) and calculate the \(p\) value. To do that, I calculate the probability that a normal distribution with the mean specified by a null hypothesis, but I use the variance as obtained above. Thus, according to the null hypothesis of \(\bar{X}=0\), \(\bar{X}\) is distributed as:
$$
H_0\text{:} \bar{X} \sim \mathcal{N}(4, {\sigma^2 \over N})
$$
The \(p\) value is therefore:
obtained_sample_mean <- mean(sample$data)
p_value <- 2*(1 - pnorm(obtained_sample_mean, mean=4, sd=sqrt(sigma_sq/n)))
p_value
## [1] 0.0008048187
Hence, the probability of obtaining something like the obtained sample mean, or something more extreme, if the null hypothesis were true, is an event that is extremely unlikely. Hence, we reject the null hypothesis in favor of the alternative hypothesis.
Note that we have calculated the \(p\) value for a two sided test, by:
- First calculating the probability of obtaining something less than the
obtained_sample_meangiven a true population mean of zero (pnorm()) - Then calculating the complement of that, reflecting the probability of obtaining something more extreme than the population mean. (This would be the
\(p\)value for a one tailed test against the alternative\(H_A: \mu > 4\)) - Then multiplying the resulting value by two, reflecting a two-sided test.
Now that we know how to do this in a simple case, we can also do the exact same thing in the context of linear regression analysis. To read about this, read the [follow-up blog post] to this present blog post. In any case, thanks for reading, and I hope this helps you understanding sampling variation.
Sampling Variation in the Context of Regression Analysis
In linear regression analysis, we often start with a linear model:
$$ Y = X \beta + \epsilon $$
Note that the only source of random variation here is the \(\epsilon\). If \(Y=X\beta\) (without \(\epsilon\)) we would always recover our \(\beta\) coefficient with certainty. But because of \(\epsilon\) can take on certain values, purely due to coincidence, in our sample, this could skew our estimate of \(\beta\), potentially far away from the true \(\beta\). Let me illustrate that with a piece of R code as well:
# Load regression libraries
library(fixest, quietly = TRUE); library(modelsummary)
# Set the parameters
epsilon <- rnorm(n=50, mean=0, sd=2)
beta <- 3
x <- runif(n=50, min=0, max=5)
# Generate Y as a function of X and Epsilon
y <- x*beta + epsilon
# Create a data.frame and plot the data points
df <- tibble(x=x, y=y)
# Plot
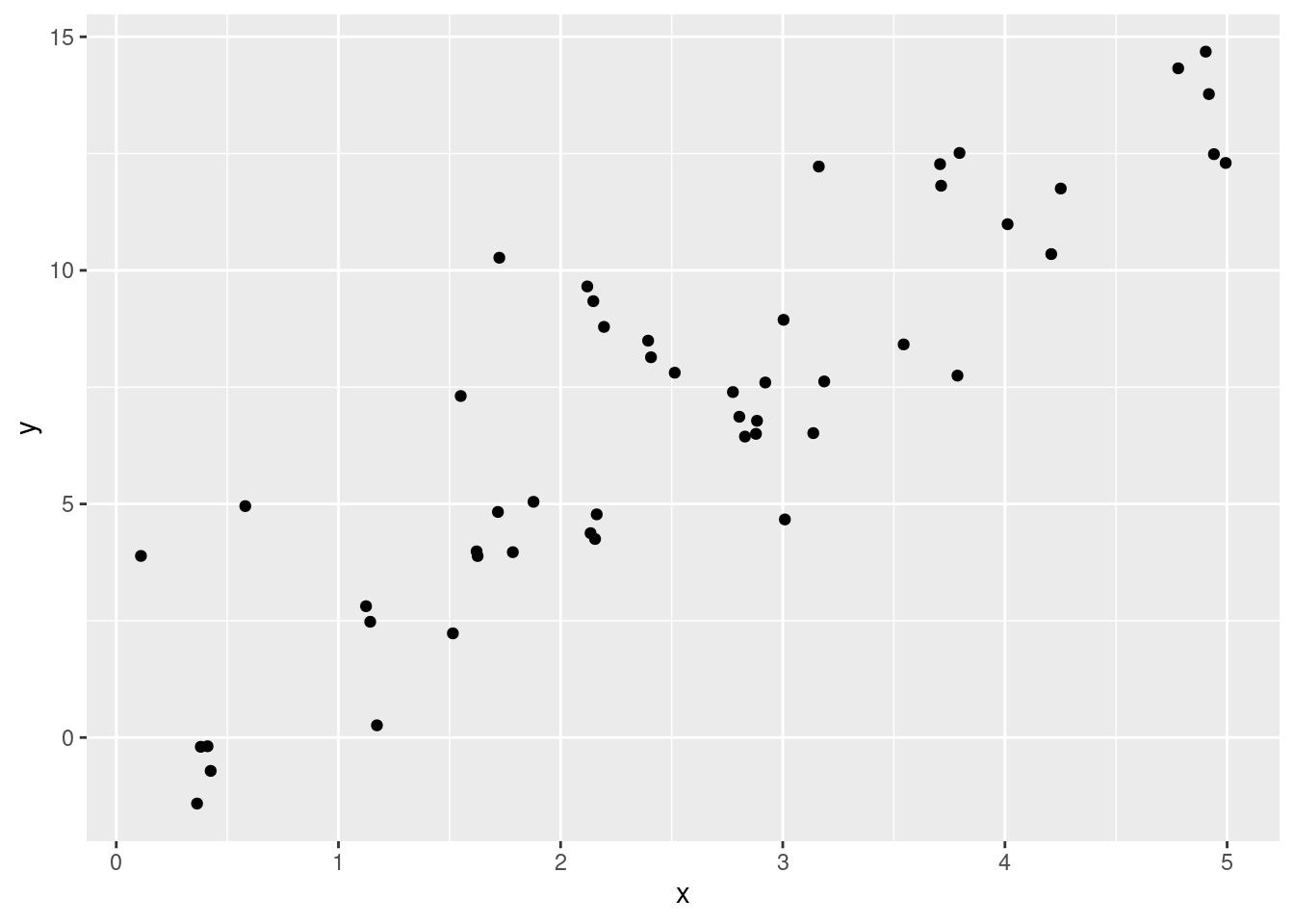
ggplot(df, aes(x=x, y=y)) + geom_point()
# Estimate a linear model
feols(y ~ x, data = df) |>
modelsummary(gof_map = "nobs")
| (1) | |
|---|---|
| (Intercept) | 0.202 |
| (0.637) | |
| x | 2.697 |
| (0.222) | |
| Num.Obs. | 50 |
As you can see, our coefficient estimate is \(3.17\) and not 3, purely due to coincidence in sampling. Hence, our \(\beta\) coefficient also exhibits sampling variation as a result of the randomness in the error term \(\epsilon\).
To illustrate that even more clearly, let me repeat the preceding piece of code 1,000 times. That is:
- Sample
\(N=50\)observations from\(\epsilon\)and\(X\). - Generate
\(Y\)from these observations - Estimate the
\(\beta\)coefficient.
And finally, plot the resulting \(1,000 \beta\) coefficients.
coefficients <- map_dbl(1:1000, ~ {
epsilon <- rnorm(n=50, mean=0, sd=2)
x <- runif(n=50, min=0, max=5)
y <- x*beta + epsilon # Remember, true beta is still 3
df <- tibble(x=x, y=y)
reg <- feols(y ~ x, data = df)
estimated_beta <- reg$coeftable$Estimate[2]
return(estimated_beta)
})
# Plot the result
tibble(coef=coefficients) |>
ggplot(aes(x=coef)) + geom_histogram()
## `stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
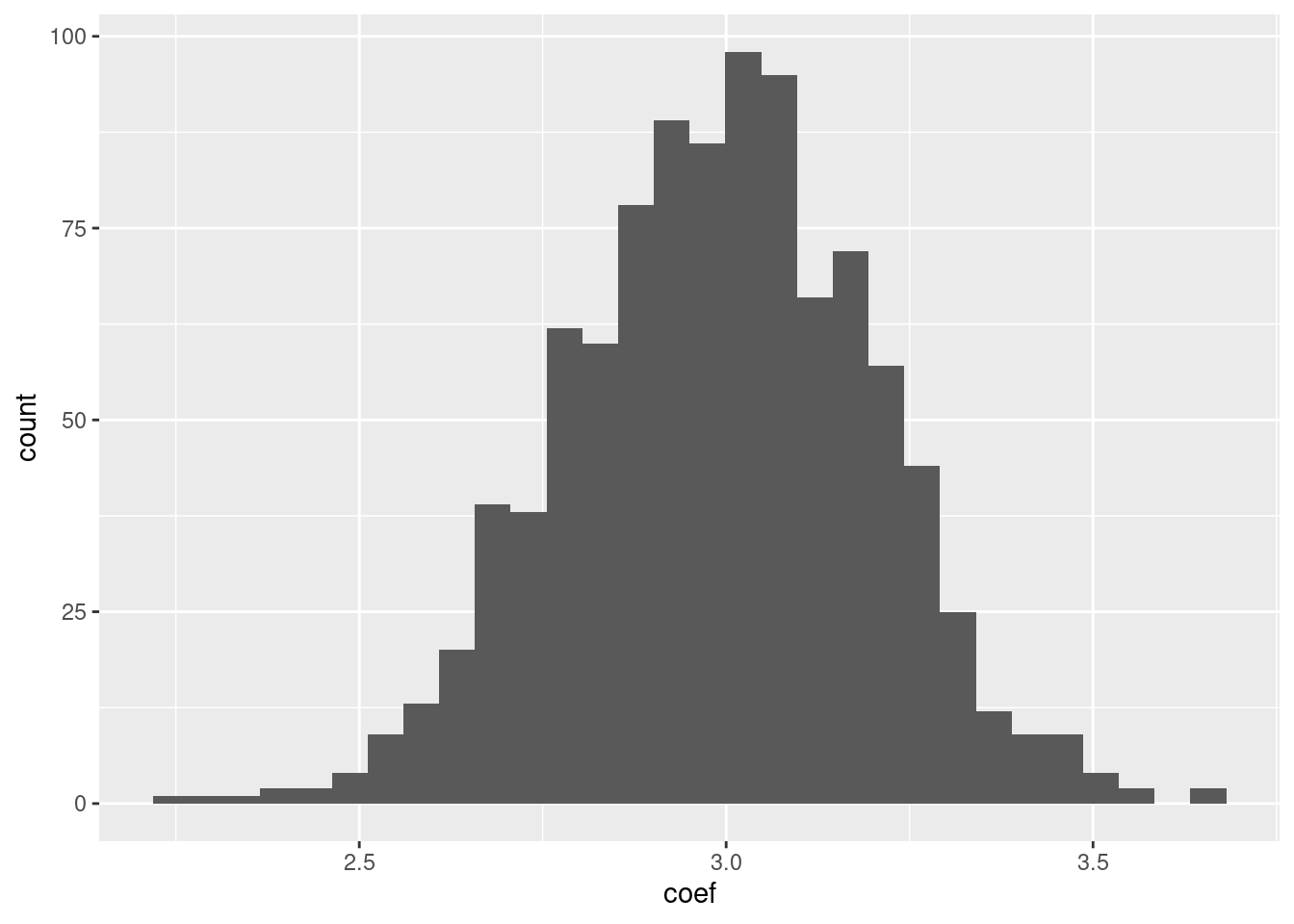
Even though on average, we estimate a \(\beta\) coefficient of 3, but out of these 1,000 times, we have, purely due to coincidental values of our \(\epsilon\) obtained \(\beta\) coefficients that are quite different from 3.
Under the assumption that our error term is normally distribution with mean 0 and variance \(\sigma^2\), we can also derive the sampling distribution for our \(\beta\) coefficients.
Hypothesis Testing?
So what are we doing when we’re doing hypothesis testing?
Conclusion
This blog post focused on the concept of sampling variation. In a very simple case, we introduced the concept by looking at a series of \(N\) i.i.d. normal variables, and derived the uncertainty surrounding our estimated mean.
Then, we did the same thing for linear regression, which turned out to be a little bit more difficult. The difficulty was that we don’t have access to the error variance parameter \(\sigma^2\), but have to make do with an estimate of that parameter. That makes it that the final sampling distribution we end up with is not normal, but \(t\) distributed.
Finally, we focused on hypothesis testing. In hypothesis testing, we hold that the true coefficient estimate is a certain number, for example, 0. Then, we use our obtained information on the sampling distribution to consider how likely it is that our actual coefficient has been obtained given that the true coefficient is zero, and the sampling distribution is the distribution we’ve estimated.
Hopefully, this background article has helped you visualizing and seeing more clearly how sampling variation, and its conceptual sibling, hypothesis testing, work. Thanks for reading! If you have any comments, mail them to a dot h dot machielsen at uu dot nl.
- Posted on:
- October 7, 2024
- Length:
- 10 minute read, 2060 words
- See Also: